
Es innumerable la cantidad de descubrimientos que se demostraron con la ley de Gauss ya que esta ley muestra de una forma matemática la distribución de una carga en una superficie altamente simétrica hace más de dos siglos. Maxwell descubrió la forma matemática de demostrar que el magnetismo y el campo eléctrico obedecen los mismos principios, ¿Cómo fue posible descubrir que el campo eléctrico y el magnetismo están interrelacionados? Carl Friedrich Gauss fue un matemático talentoso que por medio de sus conocimientos de las matemáticas y de la Geometría diferencial así como se valió del teorema de la divergencia donde en un espacio vectorial X, Y, Z fluyen líneas del campo por tanto la ley de Gauss es un resultado de un análisis multivariado del flujo eléctrico de una figura altamente simétrica como en las esferas o en los cilindros todas estas deducciones de tipo matemático comprobaron a la comunidad científica que los descubrimientos de Faraday sobre el campo eléctrico son reales, por tanto analizando la historia la matemática ha contribuido a demostrar de manera cuantitativa los fenómenos de la naturaleza y por tanto hallarle algún uso si se cuenta con la suficiente experimentación para probarlo, por tanto una de las aplicaciones que genera los descubrimientos de Faraday y las deducciones de Gauss efectiva mente es la Jaula de Faraday donde aquí se aplica un principio del campo eléctrico donde la carga que experimenta un objeto dentro de cualquier superficie conductora envolvente es nulo por tanto esta aplicación asido útil dentro de muchos inventos de tipo electrónico esta capacidad de bloquear los campos eléctricos exteriores se han aplicado:
" Desde los escudos electromagnéticos para los componentes de computadora hasta los finos recubrimientos metálicos en los vidrios de las torres de control en los aeropuertos para evitar que la radiación originada fuera de la torre afecte la electrónica en el interior de la misma"
Hewitt, P. (1999). Conceptos de Física . Wilmington: Addison-Wesley
En la figura mostramos un ejemplo de espacio vectorial
http://ffden-2.phys.uaf.edu/212_fall2003.web.dir/don_bahls/images/129fg.jpg
aqui en la ecuación vemos que el flujo eléctrico esta dado por la carga encerrada entre la constante dialéctica
http://jaibana.udea.edu.co/programas/electrica/torre.jpg
el comportamiento de las fuerzas se hacen de alguna manera más predecibles dado a la alta simetría que exige esta ley para que se apliquen estas ecuaciones que por lo general involucran la aplicación de una fuerza(electromagnética, gravitatoria) por el producto inverso de la distancia, con esta y otras ecuaciones relacionadas a la ley de gauss se pueden entender e incluso aplicar ciertos principios que gobierna la naturaleza de los flujos de fuerza, los ejemplos especificados anteriormente corresponden tan sólo una pequeña parte de las aplicaciones que pueda originar en consecuencia la comprensión de este principio matemático presente en la naturaleza
En el siguiente video se puede ver como explican brevemente la aplicación de la ley de gauss y como se usa, además señalan que cargas positivas se repelen y cargas negativas se atraen.
Voy a dar un concepto de FLUJO MAGNÉTICO: Si en un punto cualquiera P de un campo magnético consideramos un elemento de superficie perpendicular a la línea de campo en P, el flujo atreves de la superficie es el valor de la inducción magnética en P por el área del elemento de superficie será como lo observamos en la figura
En esta figura observamos el campo magnéticos creado por un imán , donde las líneas de fuerzas salen de un extremo denominado polo norte y entran por el extremo denominado polo sur.
Aplicaciones de la Ley de Gauss
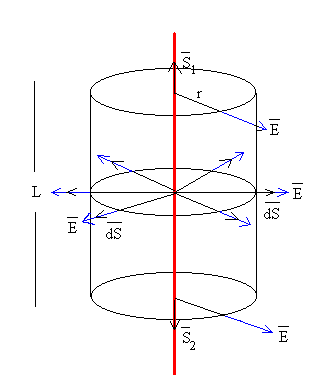 http://ffden-2.phys.uaf.edu/212_fall2003.web.dir/don_bahls/images/129fg.jpg http://jaibana.udea.edu.co/programas/electrica/torre.jpg El teorema de Gauss afirma que el flujo del campo eléctrico a través de una superficie cerrada es igual al cociente entre la carga que hay en el interior de dicha superficie dividido entre e0. Para una línea indefinida cargada, la aplicación del teorema de Gauss requiere de los siguientes pasos: .-A partir de la simetría de la distribución de carga, determinar la dirección del campo eléctrico. La dirección del campo es radial y perpendicular a la línea cargada 2.-Elegir una superficie cerrada apropiada para calcular el flujo Tomamos como superficie cerrada, un cilindro de radio r y longitud L. El mismo resultado pero de manera más sencilla. Aquí podemos observar a una superficie gaussiana que encierra una carga eléctrica
la superficie gaussiana toma la forme de la carga que rodea.
REFLEXION
Las aplicaciones de gauss nos llevan a poder calcular la densidades superficiales de cargas puntuales dentro de cascarones esféricos, cilindricos entre otros, recordemos que cada carga puntual es rodeada por la superficie gauseana que toma la forma de acuerdo a su cargas.
También aprecie que cuando se mide el campo eléctrico en cualquier parte sobre la superficie de un cascaron esférico y apuntando radialmente hacia el centro de la esfera podemos calcular con facilidad cual es la carga neta dentro de la superficie , recordemos que las cargas eléctricas en movimiento originan campos magnéticos, los cuales actúan a su vez sobre cargas eléctricas en movimiento.
Referencias
http://ffden-2.phys.uaf.edu/212_fall2003.web.dir/don_bahls/images/129fg.jpg
http://jaibana.udea.edu.co/programas/electrica/torre.jpg http://fisicanimacion.blogspot.com/ |




Este comentario ha sido eliminado por el autor.
ResponderEliminarEste comentario ha sido eliminado por el autor.
ResponderEliminarGracias por tu aporte ya se la agregue
Eliminar